Question

A chemical company makes two brand of anitifreeze. first brand is 45% pure anitifreeze , and the second brand is 70% pure anitifeeze in order to obtain 60 gallons of a mixture that contains 65% pure antifreeze , how many gallons of each brand of antifreeze must be used

Answer 1

We know that

• The first brand is 45% pure.

,

• The second brand is 70% pure.

,

• They want to obtain 60 gallons with a 65% pure.

Let's call x the amount of 70% antifreeze.

Based on the given information, we can express the following.

`0.7x+0.45\mleft(60-x\mright)=0.65(60)`

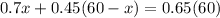
0.7x represents a 70% antifreeze. The second term represents 45% antifreeze, and 0.65(60) represents the final product. Let's solve for x.

`\begin{gathered} \text{0}.7x+27-0.45x=39 \\ 0.25x=39-27 \\ 0.25x=12 \\ x=(12)/(0.25) \\ x=48 \end{gathered}`

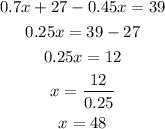
They need 48 gallons of 70% antifreeze, and 12 gallons of 45% antifreeze to get the final mixture.

Because 60-48 = 12.