Question

Which is a solution to the system the system of linear inequalities? (x, ) y-x< 4, xEI, JE I A. (3, 1) B. (4.5, 0) c. (-2, 1) D. (-3,-1)

Answer 1

Given the two inequalities below,

`\begin{gathered} 2x+y>5 \\ y-x<4 \end{gathered}`

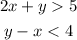
We will have to start substituting all the coordinates given to obtain the solution to the system of linear inequalities.

Checking

Option A

(3,1)

Where x = 3, y = 1

`\begin{gathered} 2(3)+1>5 \\ 6+1>5 \\ 7>5 \end{gathered}`

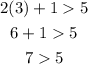
The coordinates satisfy the first inequality, let us now check the second inequality

`\begin{gathered} 1-3<4 \\ -2<4 \end{gathered}`

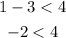
It also satisfies the second inequality, so therefore (3,1) is a solution to the inequality.

Option B

(4.5, 0)

Where x =4.5, y = 0

`\begin{gathered} 2(4.5)+0>5 \\ 9+0>5 \\ 9>5 \end{gathered}`

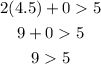
The coordinates satisfy the first inequality, let us now check the second inequality

`\begin{gathered} 0-4.5<4 \\ -4.5<4 \end{gathered}`

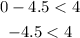
This also satisfies the two inequalities but since 4.5 is not an integer, therefore (4.5 , 0) is not a solution to the system of linear inequalities.

Option C

(-2,1)

Where x = -2, y = 1

`\begin{gathered} 2(-2)+1>5 \\ -4+1>5 \\ -3>5 \end{gathered}`

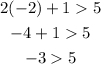
Since -3 is not greater than 5. Therefore, (-2,1) is not a solution to the system of linear inequalities.

Option D

(-3,-1)

Where x = -3, y = -1

`\begin{gathered} 2(-3_{})+(-1)>5 \\ -6-1>5 \\ -7>5 \end{gathered}`

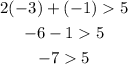
Since -7 is not greater than 5. Therefore, (-3,-1) is not a solution to the system of linear inequalities.

Hence, the solution to the system of linear inequalities is (3,1).

The correct answer is Option A.