\sqrt[4]{256}Can you simplify.

Question

`\sqrt[4]{256}`Can you simplify.

Answer 1

We want to simplify

`\sqrt[4]{256}`

To simplify, we need to find the prime factors of this number. Since it is an even number, let's start by dividing by 2.

`\begin{gathered} (256)/(2)=128 \\ \Rightarrow256=128*2 \end{gathered}`

The result still is an even number, this let us to keep dividing by 2.

`\begin{gathered} (128)/(2)=64 \\ \Rightarrow256=(64*2)*2=64*2^2 \end{gathered}`

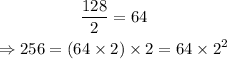
If we keep going

`\begin{gathered} (64)/(2)=32,(32)/(2)=16,(16)/(2)=8,(8)/(2)=4,(4)/(2)=2,(2)/(2)=1 \\ \Rightarrow256=(32*2)*2^2=(16*2)*2^3=(8*2)*2^4\ldots \\ \Rightarrow256=1*2^8=2^8 \end{gathered}`

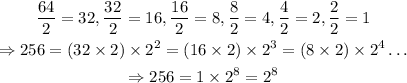
With this final equality, we have the following information:

`256=2^8`

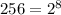
We can rewrite the root like this:

`\sqrt[4]{256}=\sqrt[4]{2^8}`

We can also rewrite this power of two like this(just using potency properties):

`2^8=(2^2)^4=4^4`

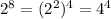
Finally rewriting our original question

`\sqrt[4]{256}=\sqrt[4]{4^4}`

The exponent and the root cancel, then we get our answer.

`\sqrt[4]{256}=4`