Solution:
The plan is to work for 40 years with a 25-year annuity.
To do this, we need to find the present value needed to achieve this in 25 years;

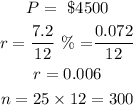
Substituting these values in the formula above,

The value that will be accumulated for 25 years annuity is $625,500.
To get the desired monthly yield, we use the future value formula for annuity.
The present value now represents the future value for the next 40years
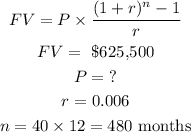
Substituting these values to get P,

Therefore, the desired monthly yield is $225.25