Question

4. To save for Malcom's education, his parents put $1,200 into a savings account whenMalcom was born in 2006. Every birthday, Malcolm's parents deposit 10% more than theprevious year.Part A: Determine the explicit formula to determine the amount of money deposited intoMalcolm's education fund. Assume a, = 2006Explicit Formula:Part B: Complete the table below.YearMoneyDeposited200612002010201420182022

Answer 1

Part A.

`P=1200(1.1)^t`

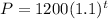
Part B

Year Money deposited

2006 1200

2010 1756.92

2014 2572.31

2018 3766.11

2022 5513.97

Step-by-step explanation:

Since the saving of each year is increasing by 10%, we can describe the situation with an exponential growth formula:

`P=P_0(1+r)^t`

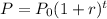
Where P0 is the initial amount, r is the growth rate and t is the number of years after 2006. So, replacing P0 by 1200 and r by 10%, which is equivalent to 0.1, we get:

`\begin{gathered} P=1200(1+0.1)^t \\ P=1200(1.1)^t \end{gathered}`

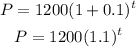
Then, to calculate the money deposited in 2010, 2014, 2018, and 2022, we need to replace t by 4, 8, 12, and 16 respectively. So, for each year, we get:

`\begin{gathered} P=1200(1.1)^4=1756.92 \\ P=1200(1.1)^8=2572.31 \\ P=1200(1.1)^(12)=3766.11 \\ P=1200(1.1)^(16)=5513.97 \end{gathered}`

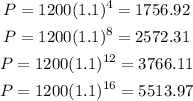
Therefore, we can complete the table as:

Year Money deposited

2006 1200

2010 1756.92

2014 2572.31

2018 3766.11

2022 5513.97