Question

Given the recursive formula for a geometric sequence find the common ratio the first five terms and the explicit formula

Answer 1

First, let find the first five terms using the recursive formula:

Then:

`a_n=a_(n-1)\cdot2`

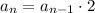
Now,

a1 = 2

For a2 :

`a_2=a_(2-1)\cdot2=a_1\cdot2=2\cdot2=4`

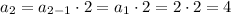
a2= 4

For a3:

`a_3=a_(3-1)\cdot2=a_2\cdot2=4\cdot2=8`

a3 = 8

For a4:

`a_4=a_(4-1)\cdot2=a_3\cdot2=8\cdot2=16`

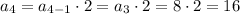
a4 = 16

For a5:

`a_5=a_(5-1)\cdot2=a_4\cdot2=16\cdot2=32`

a5 = 32

Therefore, the five first terms are 2,4,8,16,32.

Now, the common ratio is 2.

The explicit formula hast the next form:

`a_n=a_1+(n-1)d`

where d is the common ratio.

Replace using a1=2 and d=2

Therefore, the explicit formula is given by: