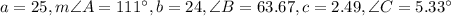
1) Let's begin by sketching out this triangle to beter gras p it:
2) So now, we can write out the Law of Sines formula:
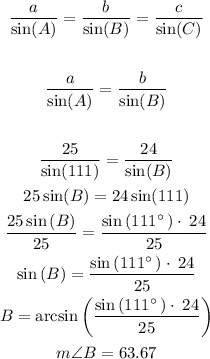
Note that we picked two ratios to find one variable. So now, let's find the measure of the angle C:
Since we know angle A, and angle B let's find the angle C by using the Triangle Sum Theorem:
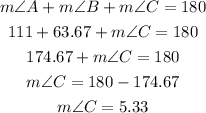
3) Now, let's find the one missing the leg c:
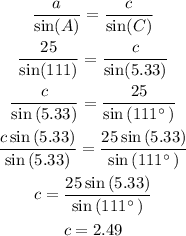
Note that we rounded off to the nearest hundredth.