Question

A 1.0 m string is under a tension of 1.0 x 102 N. The tension is increased to 1.5 x10 2 N. If the new frequency is 400 Hz, what was the original frequency?

Answer 1

Given data:

* The length of the string is L = 1 m.

* The initial value of tension in the string is,

`T_1=1*10^2\text{ N}`

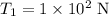
* The final value of tension of the string is,

`T_2=1.5*10^2\text{ N}`

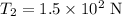
* The new frequency of the string is,

`f_2=400\text{ Hz}`

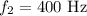
Solution:

The frequency in terms of length and tension is,

`f_1=\frac{\sqrt[]{T_1}}{L}\ldots\ldots.(1)`

The frequency in terms of length and tension in the final state is,

`f_2=\frac{\sqrt[]{T_2}}{L}\ldots\ldots\ldots..(2)`

Dividing equations (1) and (2),

`\begin{gathered} (f_1)/(f_2)=\frac{\frac{\sqrt[]{T_1}}{L}}{\frac{\sqrt[]{T_2}}{L}}_{} \\ (f_1)/(f_2)=\frac{\sqrt[]{T_1}}{\sqrt[]{T_2}} \end{gathered}`

Substituting the known values,

`\begin{gathered} (f_1)/(400)=\frac{\sqrt[]{1*10^2}}{\sqrt[]{1.5*10^2}} \\ (f_1)/(400)=\frac{1}{\sqrt[]{1.5}} \\ f_1=400*\frac{1}{\sqrt[]{1.5}} \\ f_1=326.6\text{ Hz} \end{gathered}`

Thus, the original frequency of the string is 326.6 Hz.