1 Answer

Alejandro Aburto · Answer 1 · 2023-10-24T08:46:00+0000

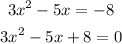
$\begin{gathered} 3x^2-5x=-8 \\ 3x^2-5x+8=0 \end{gathered}$

This equation has the next form:

To find if the equation has two complex solutions we have to check if the discriminant is negative, as follows:

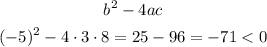
$\begin{gathered} b^2-4ac \\ (-5)^2-4\cdot3\cdot8=25-96=-71<0 \end{gathered}$

Then, the first case has two complex solutions.

In the second case,

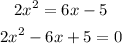
$\begin{gathered} 2x^2=6x-5 \\ 2x^2-6x+5=0 \end{gathered}$

The discriminant in this case is:

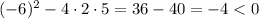
$(-6)^2-4\cdot2\cdot5=36-40=-4<0$

Then, the second case has two complex solutions.

In the third case,

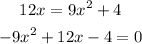
$\begin{gathered} 12x=9x^2+4 \\ -9x^2+12x-4=0 \end{gathered}$

The discriminant in this case is:

$12^2-4\cdot(-9)\cdot(-4)=144-144=0$

Then, the third case has two real solutions.

In the fourth case,

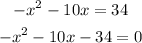
$\begin{gathered} -x^2-10x=34 \\ -x^2-10x-34=0 \end{gathered}$

The discriminant in this case is:

$(-10)^2-4\cdot(-1)\cdot(-34)=100-136=-36<0$

Then, the fourth case has two complex solutions.

Please log in or register to add a comment.