Question

Stefan was charged $223.75 interest on his bank loan for the period September 28 to December 14 of the same year. If the annual rate of interest on his loan was 5.00%, what was the outstanding principal balance on the loan during the period?

Answer 1

We have to calculate the outstanding principal of the loan.

The interest for the period is $223.75, where the period goes from September 28 to December 14.

The rate of interest is 5%, so r = 0.05.

The period includes 3 days of September, 31 days of October, 30 days of November and 14 days of December.

This is a total of 78 days.

We can now relate all the concepts as:

`I=C\cdot r\cdot t`

Where I = 223.75, r = 0.05 and t = 78/365.

We then can calculate C as:

`\begin{gathered} C=(I)/(r\cdot t) \\ C=(223.75)/(0.05\cdot(78)/(360)) \\ C\approx(223.75)/(0.05\cdot0.214) \\ C\approx(223.75)/(0.0107) \\ C\approx20911.21 \end{gathered}`

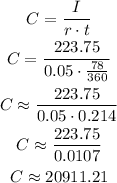
Answer: the principal is approximately $20,911.21.