Question

Calculate the following value F(-1) F(0)F(2)Given the function F(x){5x+9 X<0 5x+18 X>=0

Answer 1

Given the function

`f(x)=\begin{cases}5x+9\text{ x<0} \\ 5x+18\text{ x}\ge0\end{cases}`

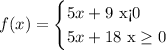
A.

To calculate f(-1)

Let us look at where f(-1) is defirned under the function f(x).

When f(x) = 5x + 9, x < 0. We can see that -1 is less than zero. Therefore, f(-1) is defined under f(x) = 5x + 9

Thus:

f(x) = 5x + 9

Substitute x = -1 into f(x)

f(-1) = 5(-1) + 9

f(-1) = -5 + 9

f(-1) = 4

B.

To calculate f(0)

f(0) is defined when f(x) = 5x + 18 (because we are told that x is greater than or equal to xero here).

`\begin{gathered} f(x)=5x+18\text{ x}\ge0 \\ \text{substitute x = 0 into f(x) above} \\ f(0)=5(0)\text{ + 18} \\ f(0)=0+18 \\ f(0)=18 \end{gathered}`

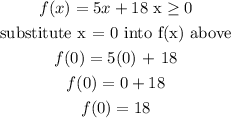
C. To calculate f(2):

f(2) is also defined when f(x) = 5x + 18 ( because x is greater than or equal to zero here and 2 is greater than 0)

Thus:

`\begin{gathered} f(x)=5x+18\text{ x}\ge0 \\ \text{substitute x=2 into f(x)=5x+18} \\ f(2)=5(2)+18 \\ f(2)=10+18 \\ f(2)=28 \end{gathered}`

Hence,

f(-1) = 4

f(0) = 18

f(2) = 28