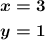Question

Solve each system of equations by graphing. If the system does not not have exactly one solution, state Wheatley it has no solution infinante solutions.

Answer 1

Since two points define a line, we can give any two values to x and replace them in the equation, then we solve for y and thus obtain the respective y-coordinates.

First line

• If x = 1:

`\begin{gathered} y=2x-5 \\ y=2(1)-5 \\ y=2-5 \\ y=-3 \\ \text{Then, the line passes through the point (1,-3)} \end{gathered}`

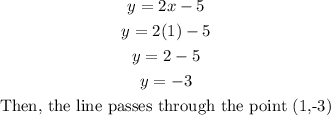
• If x = 4:

`\begin{gathered} y=2x-5 \\ y=2(4)-5 \\ y=8-5 \\ y=3 \\ \text{Then, the line passes through the point (4,3)} \end{gathered}`

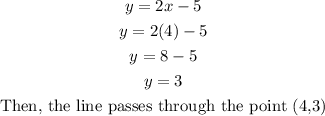
Now, we graph and join the points found:

Second line

• If x = 3:

`\begin{gathered} y=3-(2)/(3)x \\ y=3-(2)/(3)(3) \\ y=3-2 \\ y=1 \\ \text{Then, the line passes through the point (3,1)} \end{gathered}`

• If x = 0:

`\begin{gathered} y=3-(2)/(3)x \\ y=3-(2)/(3)(0) \\ y=3-0 \\ y=3 \\ \text{Then, the line passes through the point (0,3)} \end{gathered}`

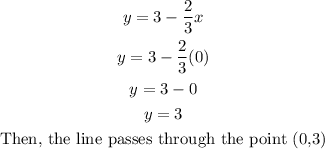
Now, we graph and join the points found:

The solution of the system of equations by graphing is the point at which both lines intersect.

As we can see, the intersection point of both lines is (3,1).

Therefore, the solution of the system of equations is

`\begin{gathered} \boldsymbol{x=3} \\ \boldsymbol{y=1} \end{gathered}`