Question

What is the best approximation for the perimeter of polygon ABCDE?

Answer 1

- The coordinates of the points read from the graph given are:

A=(-2,3)

B=(0,6)

C=(5,4)

D=(3,-1)

E=(-1,-2)

- To find the perimeter, we can use the distance between two points formula to find the lengths of each side of the polygon after which we add them up.

- Thus, we have:

`\begin{gathered} D=√((y_2-y_1)^2+(x_2-x_1)^2)\text{ \lparen Distance between two points\rparen} \\ \\ AB=√((6-3)^2+(0--2)^2) \\ AB=√(9+4)=√(13) \\ \\ BC=√((6-4)^2+(0-5)^2) \\ BC=√(4+25)=√(29) \\ \\ CD=√((4--1)^2+(5-3)^2) \\ CD=√(25+4)=√(29) \\ \\ DE=√((-2--1)^2+(-1-3)^2) \\ DE=√(1+16)=√(17) \\ \\ AE=√((3--2)^2+(-2--1)^2) \\ AE=√(25+1)=√(26) \end{gathered}`

- Thus, the Perimeter is

`\begin{gathered} P=AB+BC+CD+DE+AE \\ P=√(13)+√(29)+√(29)+√(17)+√(26) \\ P=23.598006...\approx24units \end{gathered}`

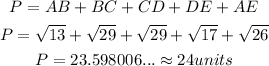
- Thus the best approximation is 24.3 units (OPTION B)