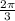Find the period and amplitude for f(x)= 2sin(3x)

Question

asked Jul 17, 2023 221k views

1 Answer

Chevone · Answer 1 · 2023-07-21T01:56:06+0000

Given:

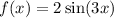
$f(x)=2\sin(3x)$

Required:

To find the period and amplitude of the given function.

Step-by-step explanation:

Given function is in the form of

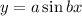
$y=a\sin bx$

Here the amplitude is

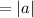
Period

$=(2\pi)/(b)$

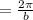
Now consider the given function

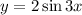
$y=2\sin3x$

Here the amplitude is

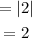
$\begin{gathered} =|2| \\ =2 \end{gathered}$

And period is

$=(2\pi)/(3)$

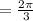
Final Answer:

The amplitude is 2 and the period is

$(2\pi)/(3)$