Answer:
v=7, 5
Step-by-step explanation:
Given the equation:
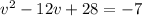
To solve for v using completing the square method, follow the steps below:
Step 1: Take the constant to the right-hand side.
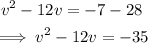
Step 2: Divide the coefficient of x by 2, square it and add it to both sides.
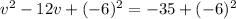
Step 3: Write the left-hand side as a perfect square.

Step 4: Take the square root of both sides.

Step 5: Solve for v.
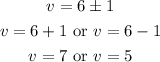
The values of v are 7 and 5.