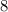Since P is a point of tangency of the circumference O, then the angle OPQ is a right angle.
Then, the triangle OPQ is a right triangle. Use the Pythagorean Theorem to write an equation for r. Then, solve that equation.
Since OQ is the hypotenuse of OPQ, then:
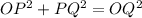
Since OP=r, OQ=r+9 and PQ=15, then:
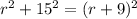
Expand the quadratic binomial on the right member of the equation:
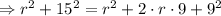
Since the term r^2 appears on both sides, simplify the equation:
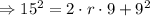
Simplify all terms and solve for r:
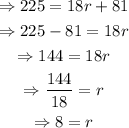
Therefore, the radius of the circumference is: