Question

I am working on this problem, and I need help with parts B and C please.

Answer 1

We have a Poisson distribution with mean μ = 4, representing the number of anomalies.

B) We have to calculate P(4 ≤ x ≤ 7).

This can be calculated as the sum of P(x = k) for k: 4, 5, 6 and 7.

We can calculate it as:

`P(4\le x\le7)=\sum ^7_(k\mathop=4)P(x=k)=\sum ^7_{k\mathop{=}4}(4^ke^(-4))/(k!)`

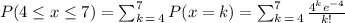
We can calculate each probability as:

`\begin{gathered} P(4)=4^4\cdot e^(-4)/4!=256\cdot0.0183/24=0.195 \\ P(5)=4^5\cdot e^(-4)/5!=1024\cdot0.0183/120=0.156 \\ P(6)=4^6\cdot e^(-4)/6!=4096\cdot0.0183/720=0.104 \\ P(7)=4^7\cdot e^(-4)/7!=16384\cdot0.0183/5040=0.06 \end{gathered}`

Now we can add them as:

`\begin{gathered} P(4\le x\le7)=\sum ^7_{k\mathop{=}4}P(x=k) \\ P(4\le x\le7)=0.195+0.156+0.104+0.06 \\ P(4\le x\le7)=0.515 \end{gathered}`

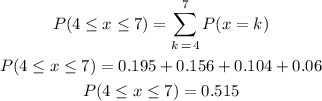
C) Now, we have to compute P(7 ≤ X) or P(X ≥ 7).

We can rewrite this as:

`\begin{gathered} P(X\ge7)=1-P(X\le6) \\ P(X\ge7)=1-\sum ^6_(k\mathop=0)P(k) \end{gathered}`

So we have to calculate the probabilities for k = 0 to k =6.

Some of them are already calculated from the proevious exercises:

`\begin{gathered} P(0)=4^0\cdot e^(-4)/0!=1\cdot0.0183/1=0.018 \\ P(1)=4^1\cdot e^(-4)/1!=4\cdot0.0183/1=0.073 \\ P(2)=4^2\cdot e^(-4)/2!=16\cdot0.0183/2=0.147 \\ P(3)=4^3\cdot e^(-4)/3!=64\cdot0.0183/6=0.195 \\ P(4)=0.195 \\ P(5)=0.156 \\ P(6)=0.104 \end{gathered}`

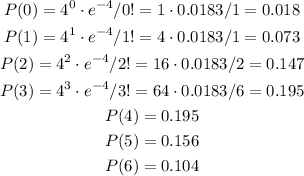
We can now add them and calculate:

`\begin{gathered} \sum ^6_(k=0)P(k)=0.018+0.073+0.147+0.195+0.195+0.156+0.104 \\ \sum ^6_(k=0)P(k)=0.888 \end{gathered}`

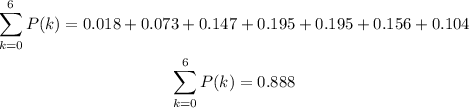
Finally, we can calculate the probability P(X ≥ 7) as:

`\begin{gathered} P(X\ge7)=1-\sum ^6_(k=0)P(k) \\ P(X\ge7)=1-0.888 \\ P(X\ge7)=0.112 \end{gathered}`

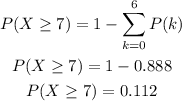
Answer:

B) 0.515

C) 0.112