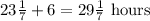Question

10. A reservoir can be filled by an inlet pipe in 24 hours and emptied by an outlet pipe in 28 hours. The foreman starts to fill the reservoir, but he forgets to close the outlet pipe. Six hours later he remembers and closes the outlet. How long does it take altogether to fill the reservoir

Answer 1

Inlet Pipe:

24 hours to fill up

So,

1/24 filled up PER HOUR

Outlet Pipe:

28 hours to empty

So,

1/28th empty PER HOUR

First, 6 hours, both were on, so fraction of reservoir that filled up would be:

`\begin{gathered} 6((1)/(24)-(1)/(28)) \\ =6((28-24)/(672)) \\ =6((4)/(672)) \\ =(24)/(672) \\ =(1)/(28) \end{gathered}`

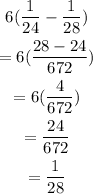
In these 6 hours, only 1/28th of the reservoir was filled up.

Now,

We have remaining: 1 - (1/28) = 27/28th of the reservoir to fill up

It fills up by inlet pipe, which has a rate of 1/24 PER HOUR.

So, the total time it will take:

`(27)/(28)=(1)/(24)t`

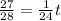
where t is the remaining time it will take. So, we solve for t:

`\begin{gathered} (27)/(28)=(1)/(24)t \\ t=((27)/(28))/((1)/(24))=(27)/(28)*(24)/(1)=(648)/(28)=23(1)/(7)\text{hours} \end{gathered}`

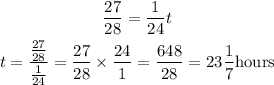
So, total time it takes to fill up the reservoir is:

`23(1)/(7)+6=29(1)/(7)\text{ hours}`