In a diagram,
Therefore, we need to find the volume of a truncated cone.
Let's define the quantities below,

Therefore, according to the question, we can identify the relations below
a) h_t=0.30h
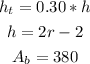
Thus,
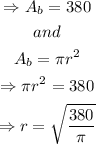
Finding h_t,
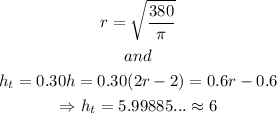
Thus, the volume of the first case is
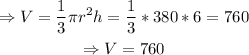
The volume when h_t=0.30h is approximately 760cm^3.
b) h_t=0.7h
Notice that A_b=380, so the result of r obtained above applies in this case too.
Obtaining h_t,
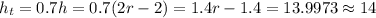
Thus,
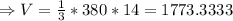
The volume when h_t=0.7 is approximately 1773.333... cm^3.