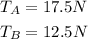Question

Find the reaction supports at Ta and TB as shown in the loaded beam.

Answer 1

`\begin{gathered} T_A=17.5N \\ T_B=12.5N \end{gathered}`

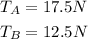
Step-by-step explanation

First, we have to make a sketch of the direction of the moments of the forces about 12m from the left in the diagram:

The sum of upward forces must be equal to the sum of downward forces. This implies that:

`\begin{gathered} T_A+T_B=20+10 \\ T_A+T_B=30N \end{gathered}`

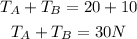
Also, the sum of clockwise moments must be equal to the counter-clockwise moments:

`\begin{gathered} (20\cdot8)+(T_B\cdot4)=(T_A\cdot12) \\ 160+4T_B=12T_A \\ \Rightarrow12T_A-4T_B=160 \end{gathered}`

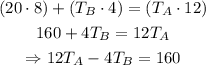
From the first equation, make TA the subject of the formula:

`T_A=30-T_B`

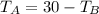
Substitute that into the second equation:

`\begin{gathered} 12(30-T_B)-4T_B=160 \\ 360-12T_B-4T_B=160 \\ -16T_B=160-360=-200 \\ T_B=(-200)/(-16) \\ T_B=12.5N \end{gathered}`

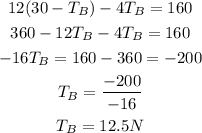
Substitute that into the equation for TA:

`\begin{gathered} T_A=30-12.5 \\ T_A=17.5N \end{gathered}`

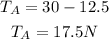
Therefore, the reaction supports at TA and TB are:

`\begin{gathered} T_A=17.5N \\ T_B=12.5N \end{gathered}`