Given
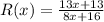
To find:
a) The domain of R(x).
b) The vertical asymptote.
c) The horizontal asymptote.
Step-by-step explanation:
It is given that,
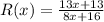
a) Consider
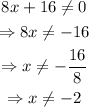
Hence, the domain of R(x) is,
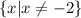
b) To find, the vertical asymptote set the denominator equal to 0 and solve for x.
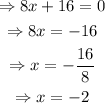
Hence, the vertical asymptote is x=-2.
c) To find the horizontal asymptote set y as the fraction of the coefficients of x in the numerator and the denominator.
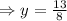
Hence, the horizontal asymptote is 13/8.
Thus,
a) The domain is,
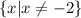
b) The vertical asymptote is x=-2.
c) The horizontal asymptote is y=13/8.