Question

Write one quadratic equation that forms a graph through the points (-4,2) and (1,2) and has aminimum value at the vertex.

Answer 1

The general form of a quadratic formula is

`f(x)=ax^2+bx+c`

where a,b and c are constants. Also, note that a is a constant that helps to determine the shape of the function. As we want that the vertex is a minimum, we are in the following situation

so, this adds the restriction that a>0.

Now, we are given the points (-4,2) and (1,2). We can replace this values in our function. Let us do that with (-4,2). So we get

`a(-4)^2+b(\text{ -4)+c=2}=16a\text{ -4b+c}`

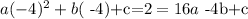
if we do that with the other point we get

`a(1)+b(1)+c=2=a+b+c`

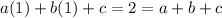
so if we make this two equations equal, we have

`16a\text{ - 4b+c = a+b+c}`

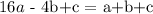
so if we subtract c on both sides, we get

`16a\text{ -4b=a+b}`

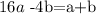
we can subtract a and b from both sides, so we get

`16a\text{ -4b -a -b =15a -5 b=0}`

so if we divide both sides by 5 we get

`3a\text{ - b=0}`

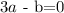
This means that we can give values to a and b freely. Recall that a must be positive. So let us choose a=1 and b=3. So our equation becomes

`x^2+3x+c`

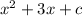
Now we need to give values for c. Note that if x = -4, we have that

`(-4)^2+3(\text{ -4)+c=16 -12 + c=2=4+c}`

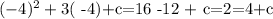
so, we subtract c 4 from both sides and we get

`c=2\text{ -4= -2}`

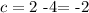
So our equation becomes

`f(x)=x^2+3x\text{ - 2}`

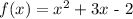
Let us check that it passes through the other point. Note when x=1 we have

`1^2+3\cdot1\text{ -2 = 1 +3 -2 = 4 -2 =2}`

so this equation fulfills the task