SOLUTION
Given the question in the image, the following are the solution steps to answer the question.
STEP 1: Write the symbolic representation of both statements
For statement 1
"If a layer of snow is not below us" is represented as:
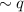
"The truck is on the road" is represented as:

Therefore statement 1 is represented as:
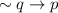
Statement 2 is represented as:
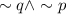
STEP 2: Complete the table
Conditional: The conditional of q by p is "If p then q" or "p implies q" and is denoted by p q. It is false when p is true and q is false; otherwise it is true.
STEP 3: Determine if the statements are equivalent
Since the two statements produce different outcomes as seen in the truth table in Step 3, it can be inferred that:
Statement 1 and and statement 2 are not equivalent. This is because the truth value statement 1 is different from the truth value of statement 2 for at least one true-