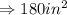Solution:
To calculate the surface area, we will use the formula below
The lateral surface area of a cuboid is the value of the surface area of a cuboid excluding its top and bottom surfaces. The formula for the lateral surface area of a cuboid is expressed as,
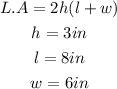
By substituting the values, we will have
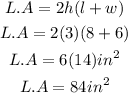
Hence,
The lateral area is
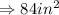
Part B:
Since the shape of the cuboid is a rectangle, to figure out the area of the single base, we will
use the formula below
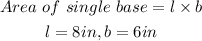
By substituting the values, we will have
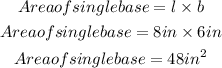
Hence,
The area of the single base is
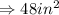
Part C:
To figure out the total surface area of the cuboid, we will use the formula below

Hence,
The total surface area is