ANSWER
You will earn $1903593 in the first investment than the second investment
EXPLANATION;
Given that;
For the first investment;
Prinicipal = $23, 000
time = 40 years
interest rate = 12%
For the second investment
Principal = $23, 000
time = 40 years
interest rate = 6%
Follow the steps below to find the amount of each investment after 40 years
Note that; the investment was compounded annually
Hence, n = 1
Write the compound interest formula

For the first investment

For the second investment
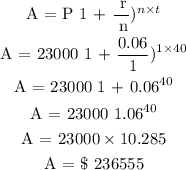
Subtract the total amount realized in investmment 2 from investment 1
So, we have
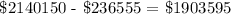
Therefore, you will earn $1903593 in the first investment than the second investment