Question

The pool company developed new chemicals that transform the pH scale. Using the pH function p(t) = −log10t as the parent function, explain which transformation results in a y-intercept and why. You may graph by hand or using technology. Use complete sentences and show all translations on your graph. p(t) + 1 p(t + 1) −1 p(t)

Answer 1

- Transformation 1 has no y-intercept

- Transformation 2 has a y-intercept of -2

SOLUTION

Problem Statement

We are told the PH of a pool is given by the function:

`p(t)=-\log 10t`

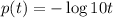
New chemicals transform this function and we are asked to find which transformation results in a y-intercept and we are also asked to show them graphically.

The translations are:

`\begin{gathered} p(t)+1=f(t)=-\text{log(}t)+1\text{ (Transformation 1)} \\ P(t+1)-1=f(t)=-\log 10(t+1)-1\text{ (Transformation 2)} \end{gathered}`

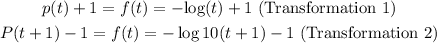
Method

Y-intercept

To find the y-intercepts of the graphs, we simply need to find the value of the p(t) when t = 0.

Plotting the graphs:

To plot the graphs, we shall apply a graphing calculator.

Solution

Transformation 1:

i. Y-intercept:

`\begin{gathered} f(t)=-\log (t)+1 \\ put\text{ t=0} \\ f(0)=-\log (0)+1 \\ \\ \text{But we know that,} \\ \lim _(t\to0)\log (t)\to-\infty \\ \therefore\lim _(t\to0)-\log (t)\to\infty \\ \\ \therefore\lim _(t\to0)f(t)=\lim _(t\to0)(-\log (t)+1)\to\infty \end{gathered}`

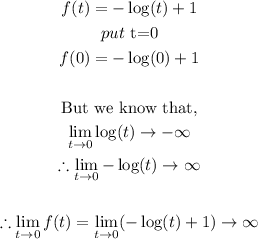
Thus, we can see that the y-intercept of f(t) tends towards infinity and since infinity is not on the Real Number line, we can conclude that this transformation has no y-intercept

ii. Plotting Transformation 1:

The graph of Transformation 1 is given below:

Transformation 2:

i. Y-intercept:

`\begin{gathered} f(t)=-\log 10(t+1)-1 \\ \text{put t=0} \\ f(0)=-\log 10(0+1)-1 \\ f(0)=-\log 10-1 \\ \\ \text{ We know that }log10=1 \\ \therefore f(0)=-(1)-1=-1-1 \\ \\ f(0)=-2 \end{gathered}`

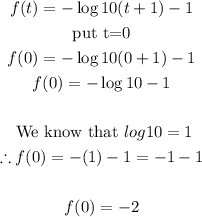
Thus, the y-intercept of this transformation exists and it is -2.

ii. Plotting Transformation 2

Final Answer

- Transformation 1 has no y-intercept

- Transformation 2 has a y-intercept of -2