Question

Find the equation of the line that is perpendicular to the given line and passes through the given point in Slope-intercept form

Answer 1

ANSWER and EXPLANATION

We want to find the line that is perpendicular to the given equation and passes through (2, 3).

The given equation is -(1/3)x + 5

The slope of any line perpendicular to another line is the negative inverse of the slope of that line.

The slope of the equation is -1/3.

Therefore, the slope of the line we are looking for is:

`\begin{gathered} (-1)/((-1)/(3))\text{ = -1 }\cdot\text{ -}3 \\ =\text{ 3} \end{gathered}`

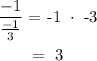
We can use the point-slope form to find the equation of the line:

y - y1 = m(x - x1)

where (x1, y1) is the point the line passes through

This means that the equation of the line is:

y - 3 = 3(x - 2)

This is the equation in point-slope form

Simplifying:

y - 3 = 3x - 6

y = 3x - 6 + 3

y = 3x - 3

That is the equation of the line in Slope Intercept form.