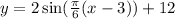Question

Help with math question precalculus A city averages 14 hours of daylight in June (the longest days) and 10 in December (the shortest days). Assume that the number of hours of daylight varies sinusoidal over a period of twelve months. Use the data above to find the following:Amplitude -Vertical shift-B value-Period- Choices Pi/12210Up 1212 months Pi/68Y=2sin(pi/2 x)+12Pi/84Y=12 sin(pi/4 x)+10

Answer 1

Given that:

Maximum hours = 14 hours

Minimum hours = 10 hours

Period = 12

Find amplitude.

`\begin{gathered} \text{Amplitude, a =}(\max -\min )/(2) \\ =(14-10)/(2) \\ =(4)/(2) \\ =2 \end{gathered}`

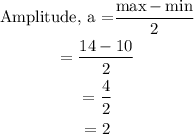
Find vertical shift, k.

`\begin{gathered} k=(\max +\min )/(2) \\ =(14+10)/(2) \\ =(24)/(2) \\ =12 \end{gathered}`

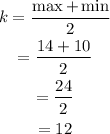
Find b from the formula

`P\text{eriod}=(2\pi)/(b)`
`\begin{gathered} 12=(2\pi)/(b) \\ b=(2\pi)/(12) \\ =(\pi)/(6) \end{gathered}`

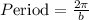
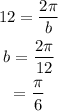
The june month means x = 6 has maximum daylight hours. So, we need to shift he maximum at x = 6.

Then h = 3.

Plug the obtained values into the formula:

`y=a\sin (b(x-h))+k`

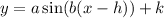
where y gives the number of daylight hours and x is the number of months since January.

`y=2\sin ((\pi)/(6)(x-3))+12`