Let's say first that duration of plan A is a, and duration for plan B is b.
We can now establish 2 equations. One for Wednesday and one for Thursday.
On Wednesday, frank trained clients for a total of 7 hours, being 3 clients with plan A, and 8 with plan B. Then:
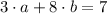
On Thursday, frank trained clients for 6 hours, being 5 clients with plan A, and 2 clients with plan B. Then:
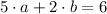
Now we have a system of 2 equations and 2 unknowns:
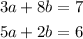
It will be easy to solve the system by reduction method. We can eliminate terms 8b and 2b mmultiplying the second equation by -4:
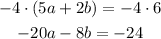
Now, the system is:

Combining two equations (adding them), we have:
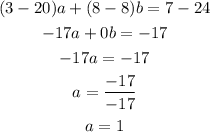
Now, we know that plan A lasts 1 hour.
We can use any equation to solve for b, knowing that a = 1.
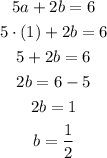
Now, we know plan B lasts half an hour (1/2 hour).