Let a, b, and c be the lengths of the sides (in ft) of the triangle.
Since one side of a triangle is twice the smallest side, the third side is four feet more than the shortest side and the perimeter is 12 feet, then f c is the length of the smallest side, then we can set the following system of equations:
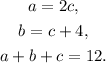
Substituting the first and second equations in the third one we get:

Adding like terms we get:

Subtracting 4 from the above equation we get:
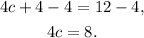
Dividing the above equation by 4 we get:
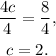
Finally, substituting c=2 in the first and second equations we get:
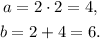
Answer: The lengths of all three sides (in feet) are: 2, 4, and 6.