In this case, we'll have to carry out several steps to find the solution.
Step 01:
Data
P(x) = x^4 + x^3 - 2x - 12
factor = x + 2
Step 02:
Factor Theorem
P(a) = 0
x + 2
P(-2) = 0
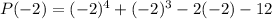
P(-2) = 16 - 8 + 4 - 12
P(-2) = 0
The answer is:
P(-2) = 0
x + 2 is a factor of P(x)