18.
To model this situation, we can use an exponential equation:
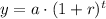
Where a is the initial value, t is the time in years and r is the rate of increase or decrease.
So for this case, we have a = 25000 and r = -0.35 (negative because the value decreases each year).
Therefore the equation is:
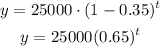
19.
After 3 years (that is, for t = 3), the price of the vehicle will be:

The price will be $6,865.62.