Question

Two blocks A and B of masses 2kg and 4kg respectively are connected by a light inextensible string passing over a pulley fixed at the top of the incline as shown in figure. The coefficient of friction between block A and surface of the incline is 0.2. Find the acceleration of the system when released and the tension in the string.

Answer 1

Given:

The mass of the block A, m_A=2 kg

The mass of the block B, m_B=4 kg

The angle of inclination, θ=30°

The coefficient of the friction between block A and the surface, μ=0.2

The acceleration due to gravity, g=9.8 m/s²

To find:

The acceleration of the objects and the tension in the string.

Step-by-step explanation:

The forces acting on block A are the tension in the string directed up the incline, the friction, and the gravitational force acting down the incline.

Thus the net force acting on the block A is given by,

`\begin{gathered} m_Aa=T-m_Ag-f \\ =T-m_Ag\sin\theta-\mu* m_Ag\cos\theta \end{gathered}`

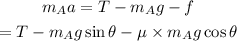
Where a is the acceleration of the system and T is the tension in the string.

On rearranging the above equation,

`T=m_Aa+m_Ag\sin\theta+(\mu* m_Ag\cos\theta)\text{ }\to\text{ \lparen i\rparen}`

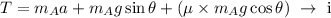
The forces acting on block B are the downward gravitational force and the upward tension in the string.

Thus the net force acting on block B is given by,

`m_Ba=m_Bg-T`

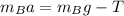
On rearranging the above equation,

`T=m_Bg-m_Ba\text{ }\to\text{ \lparen ii\rparen}`

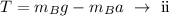
From equations (i) and (ii),

`m_Aa+m_Ag\sin\theta+(\mu* m_Ag\cos\theta)=m_Bg-m_Ba`

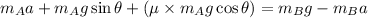
On rearranging the above equation,

`\begin{gathered} m_Aa+m_Ag\sin(\theta)+(\mu m_Ag\cos(\theta))=m_Bg-m_Ba \\ \implies m_Aa+m_Ba=m_Bg-m_Ag\sin(\theta)-(\mu m_Ag\cos(\theta)) \\ \implies(m_A+m_B)a=g[m_B-m_A\sin(\theta)-(\mu m_A\cos(\theta))] \\ \implies a=(g[m_B-m_A\sin(\theta)-(\mu m_A\cos(\theta))])/(m_A+m_B) \end{gathered}`

On substituting the known values in the above equation,

`\begin{gathered} a=(9.8[4-2\sin30\degree-(0.2*2*\cos30\degree)])/(4+2) \\ =4.33\text{ m/s}^2 \end{gathered}`

On substituting the known values in the equation (ii),

`\begin{gathered} T=4*9.8-4*2 \\ =31.2\text{ N} \end{gathered}`

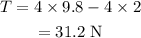
Final answer:

The acceleration of the system is 4.33 m/s²

The tension in the string is 31. 2 N