![\begin{array}{rrrrr} 10x&-&18y&=&2\\ -5x&+&9y&=&-1 \end{array}~\hfill \implies ~\hfill \stackrel{\textit{second equation }* 2}{ \begin{array}{rrrrr} 10x&-&18y&=&2\\ 2(-5x&+&9y&)=&2(-1) \end{array}} \\\\[-0.35em] ~\dotfill\\\\ \begin{array}{rrrrr} 10x&-&18y&=&2\\ -10x&+&18y&=&-2\\\cline{1-5} 0&+&0&=&0 \end{array}\qquad \impliedby \textit{another way of saying \underline{infinite solutions}}]()
if we were to solve both equations for "y", we'd get
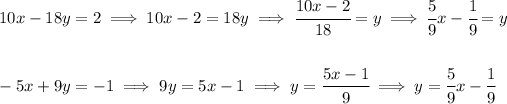
notice, the 1st equation is really the 2nd in disguise, since both lines are just pancaked on top of each other, every point in the lines is a solution or an intersection, and since both go to infinity, well, there you have it.