Answer:
a) Geometric Sequence
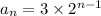
b) Arithmetic Sequence
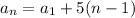
Step-by-step explanation:
a) We have the sequence: 3, 6, 12
For arithmetic sequences, the difference between successive terms are equal:
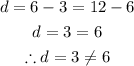
This is not an arithmetic sequence
For geometric sequences, the ratio of successive terms are found to be equal:
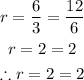
This is a geometric sequence
Its formula is thus given as:

b) We have the sequence: 3, 8, 13
For arithmetic sequences, the difference between successive terms are equal:
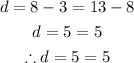
This is an arithmetic sequence
Its formula is thus given as:
