Question

How can you change the inequality signs, such that there is no shaded solution.

Answer 1

In our problem we have two regions. They are

`\begin{gathered} x^2+y^2\geq1 \\ x^2+y^2<9 \end{gathered}`

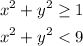
Both regions represents a circle. The first region

`x^2+y^2\geq1`

has a circle with a radius equals to 1 as the boundary, and our region is the boundary itself plus all the values with a bigger radius than 1.

The second region is

`x^2+y^2<9`

has a circle with a radius equals to 3 as the boundary, and our region is composed of all values with a radius less than 3.

Combining those two inequalities, their interception is the region between the circles plus the circle with radius equals to 1.

If we change the sign only of the first inequality, we're going to have the region inside of the minor circle as the interception of the inequalities, and if we change the sign of the second inequality only we're going to have the region outside the bigger circle as the interception. To have no solution, we have to change both signs

`\begin{gathered} x^2+y^2\leq1 \\ x^2+y^2>9 \end{gathered}`

We can't have simultaneously a point inside the minor circle and outside the bigger circle.