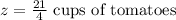We can solve this problem by applying the rule of three.
6a) We have
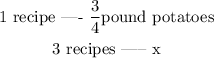
where x correspond to the pound potatoes for 3 recipes.
Then, x is given by
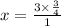
which gives
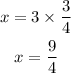
Therefore, the answer for 6a is
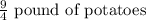
6b)
Similarly,
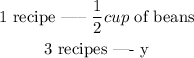
where y corresponds to the cups of beams for 3 recipes. Then, y is given by
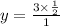
which gives
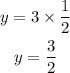
Therefore, the answer for 6b is
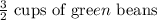
6c)
In this case, we have
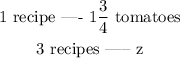
where z corresponds to the number of cups of tomatoes for 3 recipes. Then, z is given by
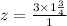
which gives
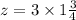
In order to obtain the product, we need to convert the mixed fraction into a simple fraction form, that is
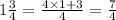
then, we have
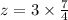
And the answer for 6c is