Question

Three horizontal forces are pulling on aring, at rest. F1 is 100 N at a 45.0° angle,and F2 is 135 N at a 160° direction. What isthe x-component of F3?F2„F1'F3X-component (N)Enter

Answer 1

As, the ring is in rest, the net force acting on the ring will be zero.

Hence, the x component of force will be zero. Therefore,

`F_1(x)+F_2(x)+F_3(x)=0`

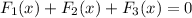
Therefore the x componet of F3 is given as,

`F_3(x)=-(F_1(x)+F_2(x))`

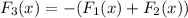
Substituting all known values,

`\begin{gathered} F_3(x)=-\lbrack100\cos (45^o)-135\cos (20^o)\rbrack \\ =-\lbrack70.71-126.86\rbrack \\ =56.15\text{ N} \end{gathered}`

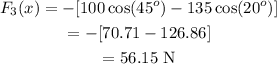
Therefore, the x component F3 is 56.15 N.

The y-component of F3 is given as,

`F_3(y)=-(F_1(y)+F_2(y))`

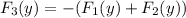
Therefore,

`\begin{gathered} F_3(y)=-(100\cos (45^o)+135\sin (20^o)) \\ =-(70.71+46.17) \\ =-116.88\text{ N} \end{gathered}`

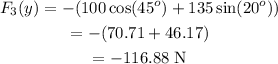
Therefore, y-component of F3 is -116.88 N (which shows that F3 is in downward direction).