Question

Find three consecutive odd integers such that the sum of three times the first, one times the second, and two times the third is 424. List the numbers in order from smallest to largest.

Answer 1

Let us suppose that n is the first odd integer.

Then the second odd integer will be (n + 2)

Then the third odd integer will be (n + 4)

three times the first means 3n

one time the second means 1*(n + 2) = (n + 2)

two times the third means 2*(n + 4) = (2n + 8)

Now their sum is equal to 424 so we can write

`3n+(n+2)+(2n+8)=424`

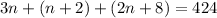
Now let us simplify the above equation

`\begin{gathered} 3n+n+2+2n+8=424 \\ 6n+10=424 \\ 6n=424-10 \\ 6n=414 \\ n=(414)/(6) \\ n=69 \end{gathered}`

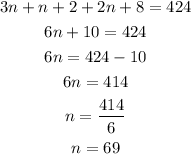
So the first odd integer is n = 69

Then the second odd integer is (n + 2) = 69 + 2 = 71

Then the third odd integer is (n + 4) = 69 + 4 = 73

Therefore, the three consecutive odd integers are 69, 71, 73.