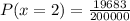Given that:
- The bin contains 100 CDs.
- Ten (10) of these CD's are defective.
- A customer randomly selects six (6) CDs.
You need to use the Binomial Distribution Formula:
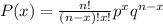
Where "n" is the number of trials, "x" is the number of successes desired, "p" is the probability of getting success in one trial, and "q" is the probability of getting a failure in one trial.
In this case, you can identify that:

Now you can substitute values into the formula:
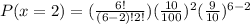
Simplifying, you get:
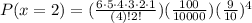
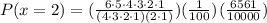
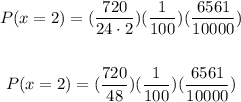
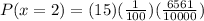
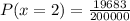
Hence, the answer is: