Answer:
m = 0.623 kg
Step-by-step explanation:
By the conservation of energy, we can write the following equation
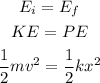
Where m is the mass, v is the speed, k is the constant of the spring and x is the compression.
Solving the equation for m, we get
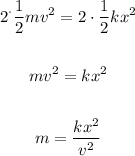
Now, we can replace k = 955 N/m, x = 3.5 cm = 0.0355 m, and v = 1.39 m/s to get

Therefore, the mass required is 0.623 kg