ANSWER
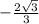
Step-by-step explanation
We want to find the value of:
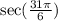
First, we can rewrite the angle by reducing it by 4π i.e. two full rotations of 2π to make the angle between 0 and 2π. The angle then becomes:
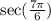
This is the same as:
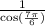
Now, we can apply the reference angle by finding the equivalent value of the angle in the first quadrant:
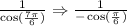
The value is negative because the reference angle is in the third quadrant and cosine is negative in the third quadrant.
Now, solving this, we have:
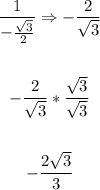
That is the answer.