Question

0.13x⁴+0.22x³-0.88x²-0.25x-0.09state the approximate roots

Answer 1

Given the polynomial:

`0.13x^(4)+0.22x^(3)-0.88x^(2)-0.25x-0.09`

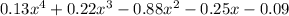
The roots of the polynomial can be said to be the x-intercept on the graph.

To find the root, equate the polynomial to zero, we have:

`0.13x^(4)+0.22x^(3)-0.88x^(2)-0.25x-0.09=0`

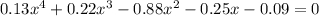
Let's graph each side of the equation.

We have the graph atteched below:

The x-intercept is the point where the line touches the x-axis, and this points of intersection are the roots of the polynomial.

Thus, from the graph, the roots of this polynomial are:

x = -3.49, and 2.08

The approximate roots are:

x = -3.5 and 2.1

ANSWER:

-3.5 and 2.1