Given:
• Product of two numbers = 1856
,
• Sum of two numbers = 90
Let's find the difference of these two numbers.
Let x represent the bigger number.
Let y represent the smaller number.
We have the system of equations:
• xy = 1856
,
• x + y = 90
Let's solve the system simultaneously using substitution method.
Rewrite the second equation for x:
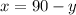
Substitute (90-y) for x in equation 1:
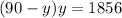
Apply distributive property:
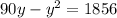
Equate the equation to zero and factor the left side:
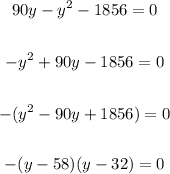
Equate the individual factors to zero and solve for y:
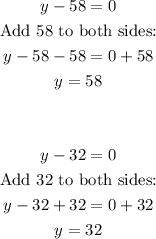
Therefore, we have:
y = 32 and 58
Since y is the smaller number, let y be 32.
x is the greater number.
x = 58.
Therefore, the two numbers are:
58 and 32.
To find the difference of the two numbers, subtract the smaller number from the greater number.
58 - 32 = 26
Therefore, the difference of the two numbers is 26.
ANSWER:
C. 26