Question

Match each pair of inverse operations.1. cubing2. multiplication3. squaring4. additionTaking the square rootTaking the cube rootDivisionSubtraction

Answer 1

The inverse of an operation is an operation that will bring it back to its initial value/form. such as the inverse of addition is subtract, sutraction can reverse addition operaation.

So,

1. Cubing; the inverse of cubing is to take the cube root.

`\begin{gathered} cube\text{ of x is;} \\ x^3 \\ \text{then taking the cube root, we have ;} \\ \sqrt[3]{x^3}=x^{} \\ so,\text{ it has reversed the operation.} \end{gathered}`

2. Multiplication; the inverse is division

`\begin{gathered} x\text{ multiply by y is;} \\ x* y=\text{ xy} \\ \text{then reversing by division with y, we have;} \\ (xy)/(y)=x \\ \end{gathered}`

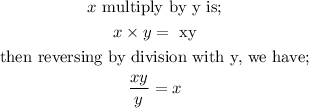
3. squaring; the inverse is taking the square root.

`\begin{gathered} \text{squaring x we have;} \\ x^2 \\ \text{reversing by square root, we have;} \\ √(x^2)=\text{ x} \end{gathered}`

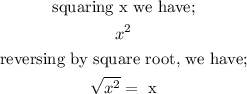
4. addition; the inverse of addition is subtraction.

`\begin{gathered} \text{add a to x.} \\ =x+a \\ \text{reversing by subtracting a, we have;} \\ x+a-a=x \end{gathered}`

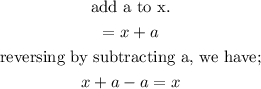
the inverse of each are below:

1. cubing -Taking the cube root



2. multiplication - Division



3. squaring - Taking the square root



4. addition - Subtraction