Solution
For this case we can do the following:
x= number of jumbo biscuits
y= number of regular biscuits
Then we can write the conditions given:
1) For the total of biscuits in a day we have
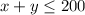
2) For the amount of flour we have:
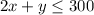
3) And we need to satisfy these other conditions:
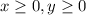
After this we have an objective function associated to the totat income and we can write:
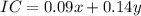
Now we need to plot the conditions to find the optimal solution:
We have 4 possible points as the solution :
(0,0) (0,200), (100,100), (150,0)
Now we evaluate the objective function for each point and we got:
IC(0,0)= 0.09*0 +0.14*0 = 0
IC(0,200)= 0.09*0 +0.14*200 = 28
IC(100,100)= 0.09*100 +0.14*100 = 23
IC(150,0)= 0.09*150 +0.14*0 = 13.5
Since we want to maximize the income then the optimal solution would be 0 jumbo buscuits and 200 normal biscuits
And the maximum income is 28
The company should make 0 jumbo and 200 regular biscuits.
The maximum income is 28.