Question

Find the equation of the line described. Write the equation in one slope-intercept form. Graph the line. Horizontal line that contains (-2,4)

Answer 1

It should be noted that the slope of a horizontal line is always zero. The equation of a line given the slope and a point can be calculated using the formula

`\begin{gathered} \text{Given slope m, and point A of coordinate} \\ A(x_1,y_1) \\ \text{The equation can be calculated using} \\ (y-y_1)/(x-x_1)=m \end{gathered}`

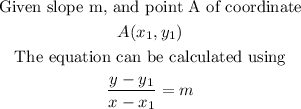
Given that the slope is zero, and coordinate (-2,4), the equation of the line would be

`\begin{gathered} \text{Given} \\ x_1=-2,y_1=4,m=0 \\ (y-y_1)/(x-x_1)=m \\ (y-4)/(x--2)=0 \\ (y-4)/(x+2)=0 \\ y-4=0(x+2) \\ y-4=0 \\ y=4 \end{gathered}`

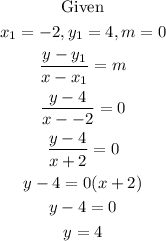
The graph of the equation y=4 is as shown below

Hence, the equation of the line is y=4 and the graph is as shown above