Question

f(x) = 4x^2 + 4x - 3Part A:Your friend claims the only way to determine the zeros without a calculator is to use the quadratic formula. You’re a teacher disagrees with your friend and says there is more than one way to determine the zeros. Explain who is correct and why.Part BDetermine the zeros of the function

Answer 1

Write out the function

`f(x)=4x^2+4x-3`

There are several ways of solving a quadratic equation. The quadratic formula, factorization, graphical method, etc.

Part A

To tell whether a quadratic equation is factorable, we use the Discriminant

`\begin{gathered} b^2-4ac \\ \text{from the equation given, } \\ a=4,b=4,c=-3 \end{gathered}`

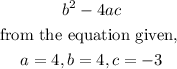
Hence

`\begin{gathered} 4^2-4(4)(-3) \\ 16+48=64 \\ \end{gathered}`

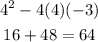
Since the discriminant is greater than zero and a perfect square hence, it is factorizable

Hence, there is more than one way to solve or determine the zeros of the function

Part B

To find the zeros of the function, we equate the f(x) to zero

`\begin{gathered} Multiply\text{ the first and last term} \\ 4x^2*-3=-12x^2 \\ \text{Then } \\ \text{ Obtain the factors that can replace the middlie term in the equation,} \\ We\text{ have } \\ -12x^2=-2x^{}*6x \\ 4x=-2x+6x \end{gathered}`

`\begin{gathered} 4x^2+4x-3=0.\text{ } \\ 4x^2+6x-2x-3=0 \\ 2x(2x+3)-1(2x+3)=0 \\ (2x+3)(2x-1)=0 \end{gathered}`

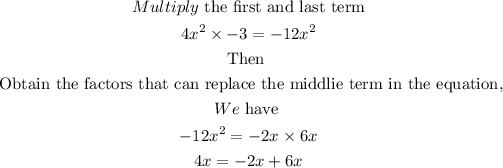
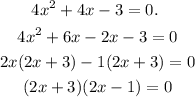
Then equate each of the factors to zero

`\begin{gathered} 2x+3=0,2x-1=0 \\ 2x=-3,2x=1 \\ \text{Divide both sides by 2} \\ x=-(3)/(2),(1)/(2) \end{gathered}`

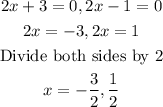
Therefore, the zeros of the function are

-3/2 and 1/2