Question

A student fires a cannonball vertically upwards with a speed of 34.0m/s. On the descent, the cannonball lands on top of a 35.0m tall building. Determine all unknowns and answer the following questions. Neglect drag and horizontal motion of the cannonball.What was the cannonball's maximum height (measured from the ground)? With what speed did the cannonball strike the building? What was the cannonball's total flight time?

Answer 1

Since the acceleration of the motion would be the gravitational acceleration this is an uniform accelerated motion; this means that we can use the following equations to solve the problem:

`a=(v_f-v_0)/(t)`
`v^2_f-v^2_0=2a(y-y_0)`
`y=y_0+v_0t+(1)/(2)at^2`

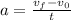
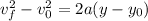
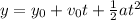
Before we begin to answer the question we need to establish a positive direction for motion and an origin. Let's assume the postive direction of motion is upward; this means that a=-9.8 m/s^2. Furthermore, let's assume that the origin is at the ground.

First question:

The maximum height happens when the cannonball reaches a velocity zero, this means that the final velocity would be zero in that point. We know that the initial velocity is 34 m/s, the acceleration and that the initial position is zero. With the variables we know we can use the second equation above to determine the maximum height:

`\begin{gathered} 0^2-34^2=2(-9.8)(y-0) \\ y=(-34^2)/(2(-9.8)) \\ y=58.98 \end{gathered}`

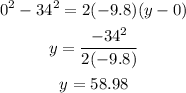
Therefore the maximum height is 58.98 m.

Second question:

To determine the velocity of the cannonball when it strikes the bulilding we think of the motion when the ball is falling. The initial velocity in this case is zero (the velocity at the maximum height), we know the acceleration, the initial position is 58.98 (the maximum height) and the final position is 35 m. Once again we can use the second equation:

`\begin{gathered} v^2_f-0^2=2(-9.8)(35-58.98) \\ v^2_f=470.008 \\ v_f=\pm\sqrt[]{470.008} \\ v_f=\pm21.68 \end{gathered}`

In this case we would have to use the minus sign for the velocity since the ball is falling; but since we are looking for the speed we drop the sign and conclude that the speed of the ball when it strikes the building is 21.68 m/s

Third question:

To determine the total flight time we need to determine the time it takes to go up and the time it takes to fall.

Time going up.

In this case the initial velocity is 34 m/s, the final velocity is zero and we know the acceleration. Using the first formula we have that:

`\begin{gathered} -9.8=(0-34)/(t) \\ t=(-34)/(-9.8) \\ t=3.47 \end{gathered}`

Hence the time it takes to go up is 3.47 seconds.

Time going down.

In this case the initial velocity is zero while the final velocity is -21.68 m/s (remember that for the velocity we need to use the correct sign), then we have that the time is:

`\begin{gathered} -9.8=(-21.68-0)/(t) \\ t=(-21.68)/(-9.8) \\ t=2.21 \end{gathered}`

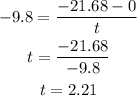
Hence the time going down is 2.21 seconds.

To determine the total time of flight we add the time it takes the ball to go up to the time it takes to fall from its maximum height to the building. This means that the total time is:

`\begin{gathered} t=3.47+2.21 \\ t=5.68 \end{gathered}`

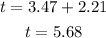
Therefore the total time of flight is 5.68 s