Question

Consider the equation ∆x = v0t + (1/2)at2. What is the variable a equal to?

Answer 1

Given the equation:

`\Delta x=v_0t+(1)/(2)at^2`

Let's determine what the variable ''a'' represents.

The given equation can be called the motion equation.

We have the variables below:

• x represents the displacement of the object

,

• v0 represents the velocity of the object.

,

• a represents the acceleration.

,

• t represents the time.

Let's rewrite the equation for a.

Rearrange the equation:

`v_ot+(1)/(2)at^2=\Delta x`

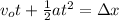
Subtract vot from both sides:

`\begin{gathered} v_0t-v_0t+(1)/(2)at^2=\Delta x-v_0t \\ \\ (1)/(2)at^2=\Delta x-v_0t \end{gathered}`

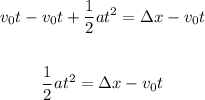
Now, Multiply all terms by 2:

`\begin{gathered} 2*(1)/(2)at^2=2(\Delta x-v_0t) \\ \\ at^2=2(\Delta x-v_0t) \end{gathered}`

Divide both sides by t^2:

`\begin{gathered} (at^2)/(t^2)=(2(\Delta x-v_0t))/(t^2) \\ \\ a=(2(\Delta x-v_(0t)))/(t^2) \end{gathered}`

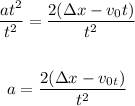
Therefore, the variable a is equal to:

2(Δx - v₀t)/t²

ANSWER:

2(Δx - v₀t)/t²